Trajectory

Research Overview for Non-Experts

Gravitational Wave science is currently one of the most exciting and flourishing areas in physics, providing a perfect meeting point between traditional pen-and-paper theory, modern numerical methods, sophisticated data analysis, and ingenious experimentation where they all contribute to answering deep questions about the fundamental nature of our universe. GWs are an essential prediction of general relativity (Einstein's theory of gravity), and by studying them we are able to push the limits of our understanding of gravity, which to this day remains the most mysterious of the four known forces.

Why do we care about gravitational waves? What's the point?

Back in the 1700 and 1800s scientists like Coulomb, Ampère, Biot, Savart, Faraday, Gauss, Maxwell, and many others made complicated contraptions and invented new mathematical ideas all to try to figure out the many bizarre patterns that were being observed in the flow of electricity and the magnetic pulls between current-carrying wires. This work culminated in (about) 1865 with Maxwell writing down the five fundamental rules of electromagnetism (called Mawell's equations and the Lorentz force law). We now know how to get all five of these rules from one rule (called the Maxwell Action), but still to this day the theory of those five rules perfectly predicts everything we observe regarding electromagnetism. All of the circuits, gadgets, and gizmos of the modern world, including the screen you are reading this on, are built on electromagnetism and all of our understanding of electromagnetism is built on Maxwell's equations. While the impact of all of this research on the world has been incalculable, Faraday wasn't studying wires and magnets in 1830 because he was dreaming of smartphones. He studied them because he was curious about the way our world works; and it is beautiful and amazing and worthwhile in-and-of-itself that everything electromagnetic ultimately comes from just 1 single equation (and one that isn't even all that complicated, by modern standards). But more pragmatically, history has proven that every time we meaningfully advance our understanding of physics, that understanding makes new technologies possible and that those new technologies make a new world possible — a world the pioneers of that understanding could never have imagined.

Einstein's theory of gravity has already proven that it can change the world — without accounting for General Relativity, GPS simply would not work. Every time you need a map app to tell you where to go, appreciate Einstein and the many scientists and engineers that took his theory and put it into practice. There are still many poorly understood aspects of Einstein's theory and a very real likelihood that we may someday find an even better theory of gravity. I believe GWs currently provide the most promising way to probe these mysteries. I do not study gravitational wave physics because I am dreaming of some super-sci-fi-time-travel-hyperspace-machine. I do it because I'm curious and gravity is cool. I can't imagine what kind of sonic-screwdriving-flux-capacitating-allspark might exist in 200 years based on physics discovered today, no more than Faraday in 1830 could have imagined the internet. I can't even predict what area of physics will make the next amazing things possible. What I can predict though is that if we want a future that is brighter than the present, we as a society have to invest in and care about science today. There will be no fruit for our children to harvest if we do not plant the seeds and tend the crops.

Okay, but why gravitational waves specifically? What even is a gravitational wave?

Credit: M. Coleman Miller & Nicolás Yunes

Gravity and electromagnetism (EM) turn out to have a lot in common. In our present understanding, gravity is really just the harder version of many of the same ideas. Electric charges are the source of electromagnetic fields. When they get moved around, they release electromagnetic waves. Think of the little visible bolt you get zapped by when you touch the wrong door handle. Many millions of little electric charges move between your finger and the knob. Those charges excite the atoms in the air and each one shoots out a burst of electromagnetic waves in the form of visible light. When something astrophysically fantastical happens like a supernova, a correspondingly fantastical spray of electromagnetic waves radiate out from the event and eventually rain down upon us, the lucky observers of the cosmic fireworks.

Einstein discovered that energy is the source of the gravitational field. When energy gets moved around, it releases gravitational waves. While obviously noticeable electromagnetic waves are pretty easy to come by in daily life (flip on a light bulb), the gravitational waves produced by moving around energy in ordinary human amounts are so small we can just ignore them. But, when something astrophysically fantastical happens like the collision and merger of two black holes, a correspondingly fantastical spray of gravitational waves radiate out from the event and as of September 14, 2015 we can now see them. Presently, we have four operational gravitational wave detectors, LIGO (Hanford, Washington), LIGO (Livingston, Louisiana), Virgo (Tuscany, Italy), and KAGRA (Hida, Japan). These projects work together under the umbrella LVK collaboration. The detectors periodically get upgraded and there also several next-generation detectors at various stages of development.

Maxwell's equations make very precise predictions about how EM waves work and over the last 150 years we have seen time and time again with higher and higher precision that those predictions are consistently actually true in the real world. If Maxwell & company had come up with different equations (some wrong ones), the predictions of those equations would not match reality. Because our experiments have become so extremely precise and they still align with Maxwell, we have great confidence in the theory. We understand EM, and because we understand it, we can use it. Einstein's GR makes very precise predictions about how GWs work and over the last 10 years we have seen so far that those predictions are consistent with what we see. But, we still have a very long way to go in terms of both theory and experiment to have anywhere near the same confidence. There are many conceivable alternatives to GR that haven't yet been ruled out by experiment. And GR, which is in a very reasonable sense the simplest possible theory of gravity, is still so complicated that in many circumstances we don't yet have good enough calculations to know exactly what we should expect from it.

I am a theorist, so the fact that there are interesting things that need to be calculated (the radiated GWs from astrophysically fantastical events) in a real physical theory (GR) to compare to real experiments that are ever improving is extremely exciting. The field is booming because we need to get better at every part of the problem. Bigger, better detectors need to be designed, built, and operated to be sensitive to all possible phenomena. Observational data needs to be analyzed more finely for us to resolve all of those phenomena. And theorists, both those making numerical simulations of the events on a computing cluster and those doing enormous amounts of algebra, need to calculate to higher and higher order of precision to have a true understanding of what we expect to see.

While the GWs that eventually reach us on Earth are very weak and require us to build enormous intricate detectors to actually appreciate them, those same waves are produced by extreme events whose theoretical details are sensitive to whatever the true theory of gravity is. Because of this, the weak GWs we see on Earth gently carry information to us about the complex inner-workings of strong gravitational fields and if we are good enough to tease out this information, we can learn more about the underlying nature of how gravity works.

What sorts of astrophysically fantastical events do we detect and why do they happen?

Credit: LIGO & Virgo

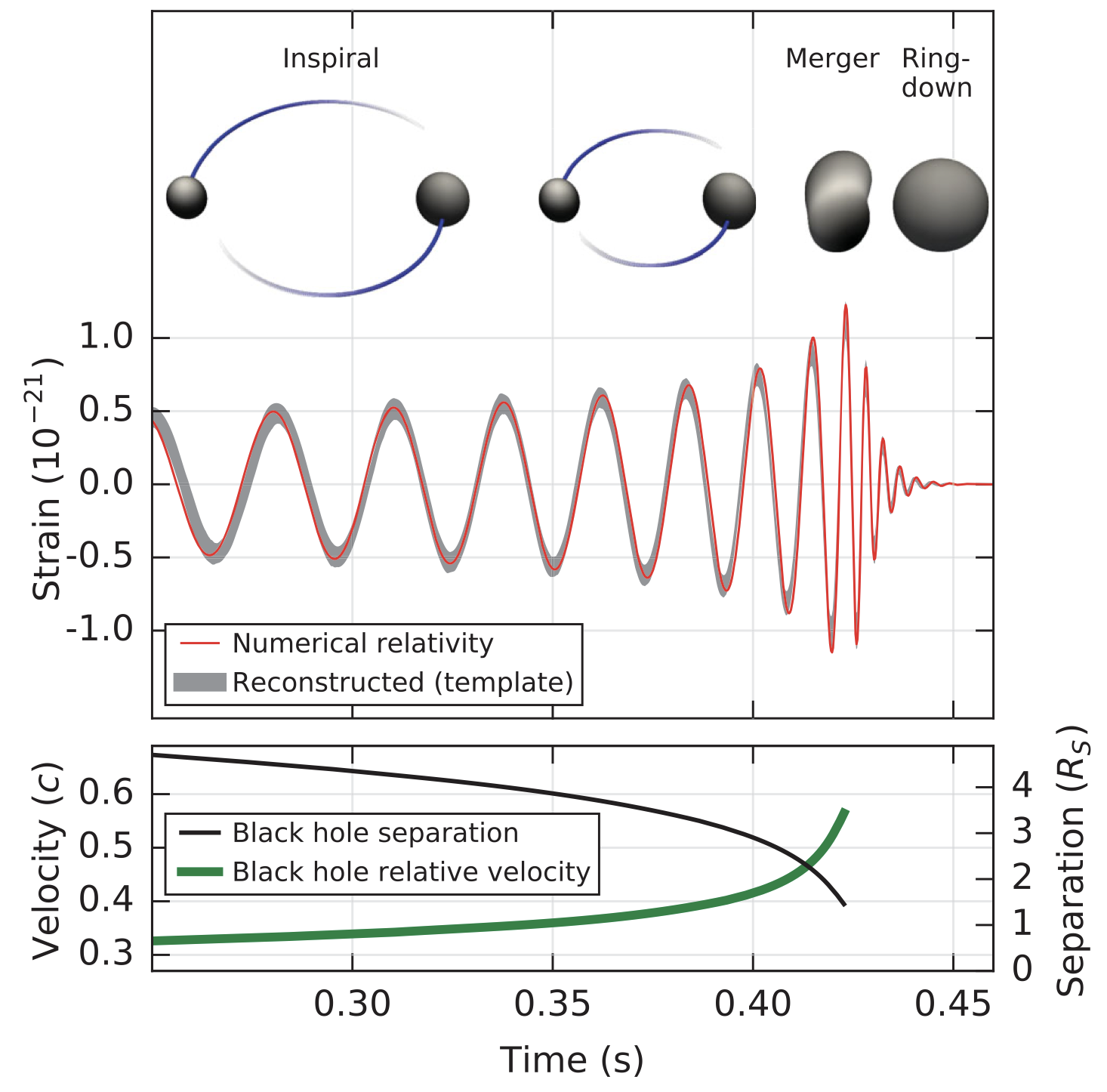
By far the most common source of detected gravitational wave events is the merger of binary black holes. A black whole is a region of space with so much energy inside of it that the gravitational field it produces is so strong that within that region even moving at the speed of light is not fast enough to escape its pull. Most (but not all) black holes form from the collapse of a dying star. There are many, many black holes in our universe. Because many star systems are binary systems, meaning there are two stars encircling each other under the influence of each other's gravitational field, they are also many Binary Black Hole systems formed after the deaths of those stars. There are also stars whose fate is to become a neutron star and so there are also Binary Neutron Star systems and even mixed binaries containing a Black Hole and a Neutron Star. As of the end of the fourth LVK observing run (O4), we have observed at least 85 BBH mergers, at least 1 BNS merger, and at least 2 BHNS mergers. There have been several more signals detected, but understanding those signals is still actively in progress.

To understand why binary systems of compact objects like BHs and NSs eventually merge, first imagine you have two objects pulled together by gravity initially sitting still with respect to each other, like a ball being dropped from rest above the ground. You know what happens; the ball and the Earth collide. If the International Space Station was at rest above the Earth, it would also fall in and the two would collide. However, the ISS is moving very fast relative to the ground. It is moving so fast that the rate at which it accelerates toward to the Earth due to gravity is balanaced by the rate at which it moves parallel to the ground below so that it never actually gets any closer, which we just call orbiting. Because the ISS whirling around the Earth is a bunch of energy moving around, the acceleration of the ISS does cause (extremely pathetically weak) GWs to be emitted. In principle if you ignore other factors you would predict that the energy of those GWs is carried away, leaving the ISS with slightly less energy itself which then makes it slow down ever so slightly and fall closer to the Earth. By being closer, the gravitational pull is then stronger, causing it to accelerate faster, and radiate energy even faster, and so on, leading to it spiralling into the Earth. Because the ISS is so much less massive than the Earth, the time it would take it to inspiral due to radiating GWs is extremely, unbelievably long and this is not a meaningful concern. Of course, this thought experiment doesn't reflect the real ISS because there are much more important effects that cause it to gradually lose energy, like atmospheric drag, and the real ISS has thrusters and gets refueled occassionally so that it can adjust its altitutde manually as necessary to stay in a comfortable orbit. A binary system of compact objects is like the ISS-Earth example, except without the many complicating factors (no atmosphere, thrusters, or refueling) and the objects are of much more similar masses to each other. The objects still orbit each other and as they do so energy is radiated away by the GWs they produce. This causes them to get closer and closer to each other, accelerating their inspiral until they collide. This can still take astronomically long, but it happens more quickly the more similar the masses of the two objects are.

As a binary of compact objects inspirals, it releases GWs that slowly get stronger as the objects get closer. Whether they are BHs or NSs, when the objects get very close they take the plunge into each other and begin to coalesce into one new black hole (due to having so much energy). This merger emits an enormous gravitational wave that makes a clear signal in our detectors on Earth. Shortly after the merger, the newly formed black hole is very blobular, wiggling and jiggling around due to the chaos of the coalescence. This vibrating further emits GWs in a process called the the ringdown. After ringing, the single remaining black hole stabilizes and ceases giving off any meaningful GW signal. While the inspiral phase lasts years and years, for the kinds of GW events we can detect currently the merger and ringdown together last under a second.

And where exactly do I fit into all of this?

Credit: Aurore Simmonet

In the inspiral phase, we know really well how to solve the kinds of equations we encounter in GR. It is hard, but possible, to do so algebraically. When the objects get too close, because of the limits of our math skills, that approach fails. Instead, we have to use computer simulations of the event. Those simulations are much more expensive and less precise during the early inspiral, where pen-and-paper (and computer algebra) methods are good. Algebraic/analytic calculations are great, because once you know the right general equation it takes no time at all to turn it into the specific numbers you need at a given moment. But, analytic calculations are limited, because sometimes the problem is just too hard for us to get the right general equation. Numerical simulations are great, because they don't miss any physical effects. But, numerical simulations are limited, because they are very resource expensive to perform and give specific results that can only be meaningfully extrapolated to understand how a subset of all the possible physical scenarios work. So, the capabilities of pen-and-paper theorists (like me) and the numerical simulation theorists (like several of my friends) complement each other. Together we can develop a clear picture of both the inspiral and the merger phase. After the merger during the ringdown, the single remaining black hole can be studied using both algebraic and numerical techniques, and we get the best results by intelligently combining these approaches.

I (along with many others) specifically study the early inspiral analytically. This means that I solve the equations that determine the motion of the two bodies and the gravitational field between them while the inspiral is going on. I do so using scattering amplitudes methods, which are theoretical tools originally invented for particle physics that have proven to be useful in far broader physics contexts than originally imagined. The basic idea is that when the black holes are very far from each other (during the early inspiral), they interact with each other effectively like particles, because their separation is much larger than their size. Particle physicists have spent decades figuring out how to do extremely precise and efficient calculations of these types of interactions, and so by applying those techniques to gravitational waves, we can get the best possible understanding of the inspiral phase. I am also particularly interested in the effects of spin in the dynamics of the inspiralling bodies. Spinning black holes are substantially more complicated and physically interesting than nonspinning black holes, and when the inspiralling bodies have significant spin it totally changes how the whole coalesence event evolves and what the radiated GW from the event looks like. While we know the correct equations of motion to use for nonspinning black holes, we don't actually know the correct equations of motion to use for spinning black holes once the spins become large. These spin effects will become increasingly more important as our detectors continue to improve.

Ultimately, my focus is on contributing to making our analytic theroetical predictions of the early inspiral phase of the binary coalesence of spinning compact objects as precise as possible. If I've done a good job explaining, that sentence should halfway make sense!

Still have more questions?

Read this excellent article: Gravitational waves: Everything you need to know

Research Details for Experts

Parameter Regimes

Credit: Ana Carvalho

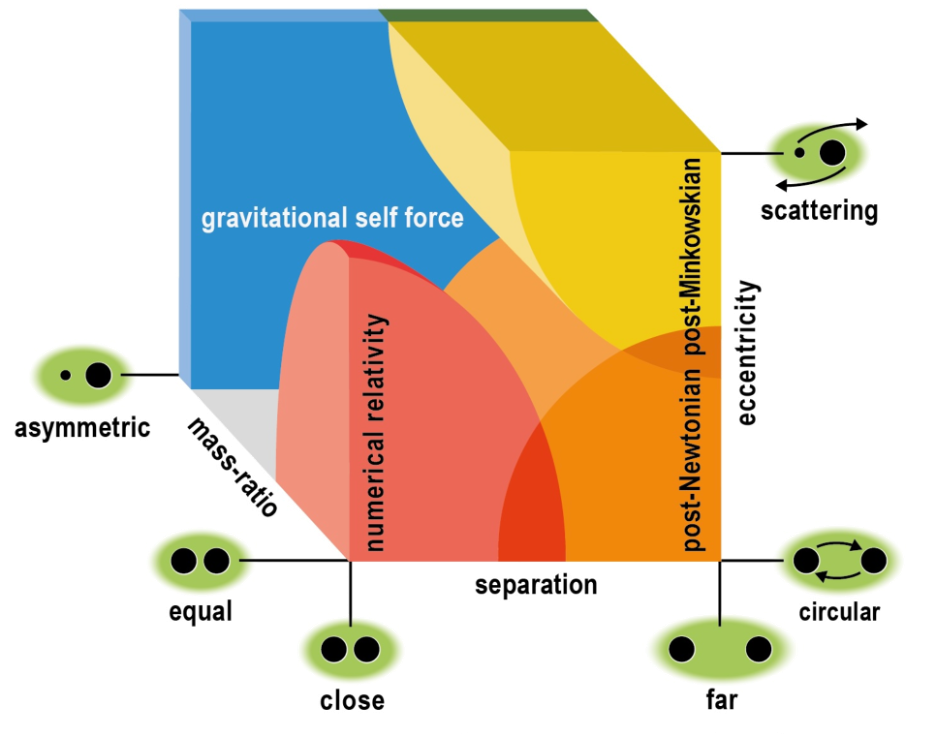
I work on perturbative analytic predictions for the general relativistic spinning two-body problem using methods from scattering amplitudes and effective field theory. To understand where my focus sits within the broader theoretical side of gravitational wave physics, I will first describe some of the several parameter regimes for the two-body problem in GR for which different methods are best-suited. Some of the various important dimensionless expansion parameters are interbody separation (the ratio of the distance between the bodies to the Schwarzschild radius of the larger body), orbital eccentricity (which is controlled by the combination of the interbody separation and the relative speed of one body to the other), mass ratio (ratio of the mass of the lighter body to that of the heavier body), and the dimensionless spin of each body (ratio of the spin-magnitude of the body to the spin-magnitude of an extremal black hole of the same mass).

My work focuses on the large separation regime, and so is valid in the early inspiral phase. For large separation, the gravitational interaction between the bodies is weak and so we can perform calculations perturbatively in powers of the gravitational constant G. In the G to 0 limit, spacetime simply becomes Minkowski space and so this framework is called the Post-Minkowskian (PM) expansion. The PM expanion fully maintains Lorentz covariance. As the inspiral goes on, due to the virial theorem the square of the relative speed of the bodies becomes inversely proportional to the separation and so it also becomes valid to work simultaneously perturbatively in powers of the speed-squared and G, counting only the total order of these quantities. This is known as the Post-Newtonian (PN) expansion, which no longer has Lorentz covariance. Analytic PM results at high orders in perturbation theory depend on very complicated functions and require the analytic evaluation of sophisticated integrals. In PN, the resulting functions and necessary integrals are much simpler and remain so at arbitrarily high order. I focus mainly on PM results.

My work treats the mass ratio of the bodies as arbitrary, though implicitly the mass ratio affects precisely how long PM results are useful. Some other analyses of the two body problem work exactly in G but perturbatively in the mass ratio. In the limit that one body becomes arbitrarily more massive than the other, the smaller body simply follows geodesics of the larger one, and geodesics in a black hole background can be solved analytically. One can then perturb in powers of the mass ratio about these geodesics. This is known as the Self-Force (SF) expansion. High orders in PM and in SF contain some overlapping data, and so calculations done in one are very helpful for matching and verifying calculations done by the other. When neither the interbody separation is large nor the mass ratio is small our analyic techniques are not capable of producing helpful answers and so Numerical Relativity (NR) is necessary. However, the parameter regimes in which analytic techniques are best happen to also be the ones in which NR is the most expensive and the least accurate, so each of these approaches has a distinct niche for which it is essential.

QFT Tools in GR

Binary Black Hole Scattering

In the 1970s, Dixon found that given any compact object in general relativity it is possible to assign to that object a (meaningfully unique) center-of-mass worldline trajectory, a total linear momentum along that worldline, and total spin-angular momentum about that worldline. He further found that these three quantities satisfy a system of equations of motion known now as the Mathisson-Papapetrou-Dixon (MPD) equations dependent on a set of higher multipole moments that are determined by the body's energy-momentum tensor. Different species of bodies will have different higher-multipole moments. If the body of interest only experiences external fields that vary slowly over its size, then at lowest order the higher multipole moments can be approximately expressed in terms of the worldline, momentum, and spin. It is possible to systematically correct this approximation by considering the next multipole moment (first would be the quadrupole) to also be independent, and so on.

If two compact objects with large interbody separation interact under gravity, they are precisely in the regime for each to be described by the MPD minimal degrees of freedom (worldline, momentum, spin). It is then possible to write a classical effective worldline action in terms of those degrees of freedom and the metric with which they interact. This action can be used for completely classical calculations, which is called the Classical Worldline (CWL) approach. Alternatively, one can treat this action as the quantity to be put into the exponent of the path integral in a quantum theory. Such a quantum theory in the classical limit will necessarily give the same classical results. This approach is known as Worldline Quantum Field Theory (WQFT). Because there have been decades worth of tools developed by particle physicists for how to perform path integral calculations directly, WQFT, while computing exactly the same things as CWL, often has an easier time recycling computational shortcuts. Alternatively still, it is possible to write down a genuine quantum field theory (in which each compact object has an associated field), including all possible interaction terms up to the given order of interest and with coefficients determined by matching the classical theory in the classical limit, and then to do genuine conventional QFT calculations directly applying all standard particle physics and scattering amplitudes techniques. The classical limit again guarantees agreement with CWL. This approach is conventional Quantum Field Theory (QFT).

CWL, WQFT, and QFT each compute the same quantities with slightly different approaches. I have and do use all of them. More important than direct calculation method are the lessons that all these methods apply from QFT to GR. In each case, we apply a Weinberg-style effective field theory approach. That is, we write down the most general action in terms of all the degrees of freedom of interest (worldline, momentum, and spin for each body and the metric) consistent with the symmetries of interest (general covariance) up to the necessary order of approximation (relevant PM order, spin order, etc) and then calculate observables by variations of that action. The standard language of 3-point, 4-point, Compton, or 5-point amplitudes in particle physics have direct physical meanings in gravitational wave physics. The 3-point amplitude is (the Fourier transform of) the energy-momentum tensor. The 4-point amplitude (the two-body to two-body amplitude) is invertibly related to the on-shell action (Hamilton-Jacobi function/eikonal phase/generator of observables). The Compton amplitude encodes the solution to black hole perturbations (the Teukolsky equation). The 5-point amplitude (two-body to two-body with an external graviton) encodes the radiated gravitational waveform from the two-body interaction.

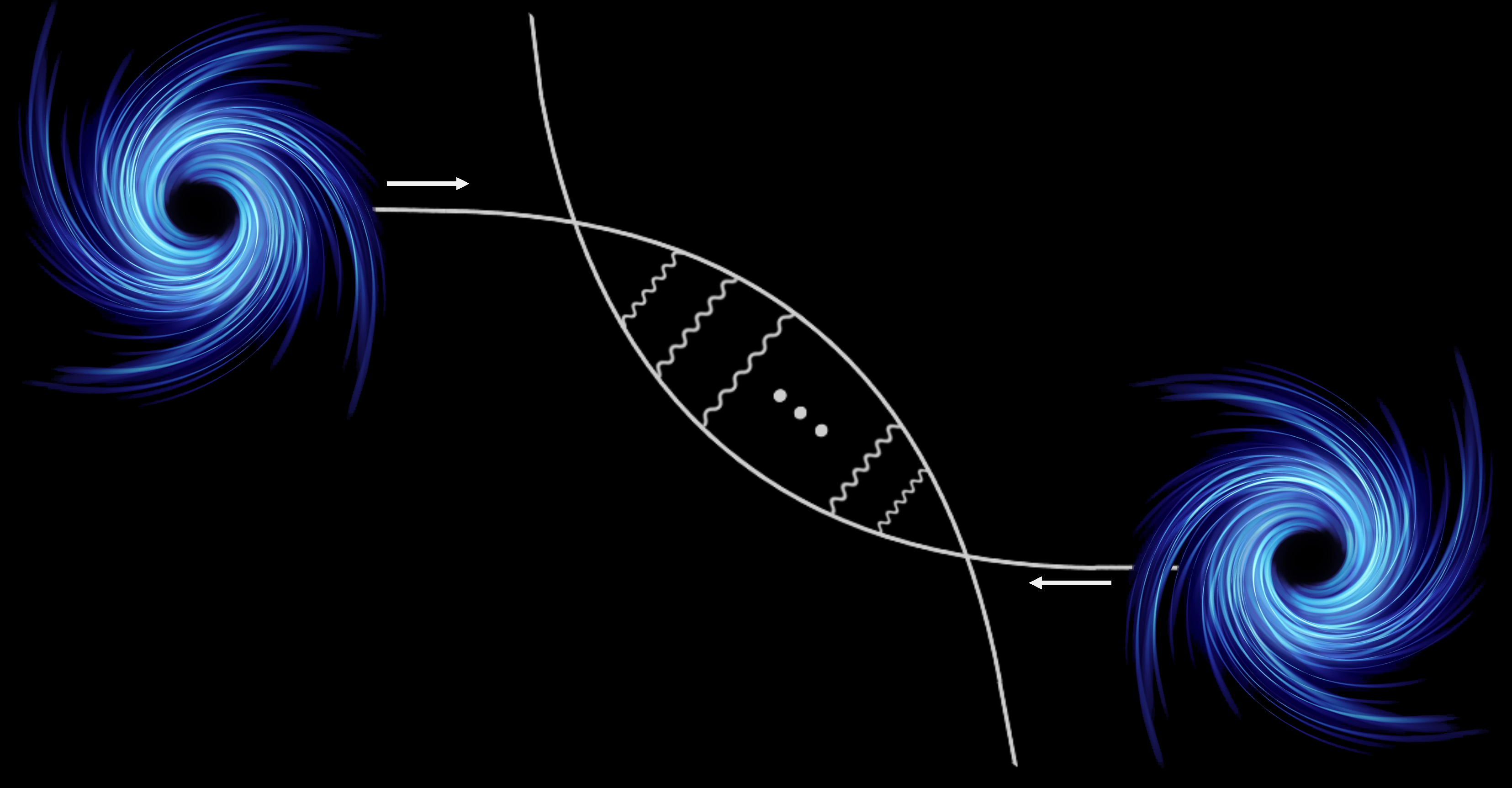
While gravitational wave physics is almost entirely about the evolution of bound orbits of binary systems, in each of these approaches we actually do calculations for unbound (scattering) trajectories. Naively, this may seem useless. However, there are several toolkits for how to map data computed about the unbound system to data for the bound system. For example, from the two-body to two-body scattering amplitude computed using QFT, one can develop an effective two-body Hamiltonian for the classical limit of the system. Because the same Hamiltonian describes all initial conditions, this Hamiltonian, though computed using unbound data, still contains the physics of the bound problem. Unbound systems are theoretically more convenient than bound orbits because it is easier to define their properties gauge invariantly. For the scattering problem, we only care about the properties of each body at past and future infinity, as well as the radiated gravitational wave at future null infinity. Because we are only interested in asymptotic quantities, we can arbitrarily redefine our fields in the spacetime bulk as long as these redefinitions become the identity transformation sufficiently quickly far away. Through field redefinitions many terms (which necessarily do not contribute independent effects to observables) can be eliminated from the action at the start, rather than observed to be redundant at the end.

Much of my work (2308, 2407, 2503) has focused on how to properly implement the spin degrees of freedom in these various approaches, as spin poses several technical challenges due to its noncanonical Poisson brackets and the need to clearly control the frame in which the spin is defined in order to propagate the correct degrees of freedom. I am also working on the development of eikonal methods, which generate observables from the classical on-shell action, to apply directly to the bound orbit rather than depend on a boundary-to-bound map. Currently the QFT approach is the most efficient at computing effective two-body Hamiltonians. I am working on developing the CWL's ability to compute the effective Hamiltonian and radiative effects through the eikonal. This is desirable because the CWL approach avoids the complicated cancelation of superclassical terms in the classical limit of the QFT.

Black Hole Equations of Motion

Equatorial discontinuity of BH field lines implies effective disk source.

There is a crucial missing step from the Weinberg-style approach given above. When we write down the effective action for our bodies, there will be an undetermined free coefficient for each term. How do we decide what values those coefficients should take? Those coefficients take different values for different species of objects. For neutron stars, they are in principle determined by whatever the appropriate equation of state for a neutron star is. For black holes, they are somehow determined by physics contained in Einstein's equations. Presently, it is not known how to fix these coefficients in general. The coefficients on terms linear in the Riemann tensor and at arbitrary order in spin are fixed by matching the 3-point amplitude of the effective theory to the linearized Kerr metric. Many classes of coefficients that are quadratic in the Riemann tensor are fixed by matching the Compton amplitude of the effective theory to solutions of the Teukolsky equation and to studying the tidal response of black holes in Einstein's theory. It is difficult to even enumerate all operators at quadratic or beyond in Riemann, but the known coefficient values for a black hole satisfy several interesting symmetry principles.

One of the major themes of my work (2311) has been to try to guess what possible symmetry principle determines the black hole effective worldline theory Wilson coefficients at general order or to find ways to extract these coefficients from matching to Einstein's equations in general. The most promising approaches are based on the Newman-Janis shift, which is an exact relationship between the Schwarzschild (nonspinning) black hole and the Kerr (spinning) black hole. Essentially, in the correct coordinates, Kerr can be understood as a complex translation of Schwarzschild. Because this property is exact in Einstein's theory, I am attempting to generalize it to dynamical black holes as a way to fix the worldline action.

The effective action used for a spinning black hole, when varied with respect to the metric, implies a particular energy-momentum tensor for the compact object. Formally in GR black holes are usually treated as vacuum solutions to Einstein's equations, because outside of the event horizon they are and we are causally disconnected with the inside. However, from the effective field theory perspective, positing a source (and its dynamics) inside the horizon is equivalent to knowing the effective action. Thus, while the true source inside a real black hole is physically irrelevant to the exterior, the effective source for the worldline is a useful computational tool. In particular, the stationary Kerr solution implies as its source a rigidly rotating disk with a particular density profile. In my work 2308, we found what matching that source requires of the worldline action. That source does not (at least in an obvious way) include the physics of how the disk responds to perturbations, and so probably cannot be used to fully fix all Wilson coefficients in the action. I am still exploring the extent to which this disk approach can be used to fix the black hole WL EFT.

Some important papers

Check out this list of many (not all) important papers in the field

Publications

• M. Alaverdian, Z. Bern, D. Kosmopoulos, A. Luna, R. Roiban, T. Scheopner, F. Teng
• arXiv:2503.03739 [hep-th]

• M. Alaverdian, Z. Bern, D. Kosmopoulos, A. Luna, R. Roiban, T. Scheopner, F. Teng
• Physical Review Letters 134 (2025) 10, 101602,  arXiv:2407.10928 [hep-th]

• T. Scheopner and J. Vines
• Journal of High Energy Physics 12 (2024) 060,  arXiv:2311.18421 [gr-qc]

• Z. Bern, D. Kosmopoulos, A. Luna, R. Roiban, T. Scheopner, F. Teng, and J. Vines
• Physical Review D 109 (2024) 4, 045011,  arXiv:2308.14176 [hep-th]

• L. de la Cruz, A. Luna, and T. Scheopner
• Journal of High Energy Physics 01 (2022) 045,  arXiv:2108.02178 [hep-th]

• T. Scheopner
• Princeton Undergraduate Mathematics Journal, Issue 1, Article 4

Talks

Teaching

I love teaching. It is one of my favorite parts of being a scientist and not having the opportunity to teach is one of my least favorite parts of being a Post-Doc. (Of course, I do still get the joy of helping mentor and teach new graduate students!) I truly believe physics can be made to make sense to physics students, that even the most difficult topics can be demystified. For the real meat of my pedagogical approach, please see my textbook (in progress).

During my PhD at UCLA I did quite a bit of teaching as a teaching assistant with on average an exceptionally high amount of responsibility for the course. The physics department offers three possible teaching awards for graduate students, an award for excellency in teaching lower division courses, a corresponding award for higher division courses, and an overall teaching assistant of the year award. I won each of these awards. I first won the lower division award for teaching the entire freshman honors physics series (1AH, 1BH, 1CH), which is an intentionally exceptionally difficult sequence and for which the usual completion rate is low (approximately 1/3). When I was the TA, the completion rate hit 2/3. Next I taught the first year physics graduate students classical mechanics and electromagnetism, for which I won the Teaching Assistant of the Year award. They also nominated me for the UCLA-wide Academic Senate Distinguished Teaching Award for which I became a finalist but ultimately I didn't win it. Afterward I taught the next batch of first year physics graduate students quantum mechanics and for that I was awarded the department's upper division teaching award.